Posted: February 4th, 2012 | Author: Gina Collecchia | Comments Off on Gibbs phenomenon
is boring, so this is going to be short. Basically, Gibbs phenomenon was discovered by a guy with the last name “Gibbs” when he saw that the Fourier series of nondifferentiable waves is least-good where the waves are not differentiable. Yeah…okay. So, when a wave has sharp edges/corners like a square wave or the absolute value function, the Fourier series representation will be infinite and have these little tail thingies sticking out at these corners and edges. Honestly, it’s not that surprising.
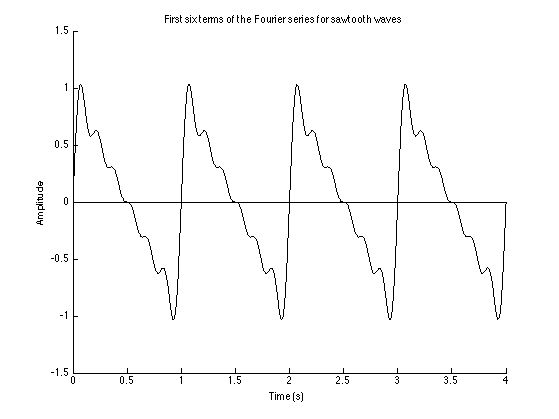
These thingies are called “Gibbs horns” or “Gibbs’ horns” or if the writer just hates checking Wikipedia, “Gibb’s horns,” and the points at which they exist are usually called “jump discontinuities,” i.e., sharp edge corner things.
Posted: October 14th, 2011 | Author: Gina Collecchia | Comments Off on A (super short) introduction to acoustic physical modeling
What does it take to understand the acoustics of a physical space, like a room or a musical instrument? You don’t have to be a musician to desire—or even require—good sound. The acoustics of an amphitheater or simple rectangular room dictate the the signal-to-noise ratios of sonic signals like speech and music. When sound reflects off of the walls, ceiling, floor, and other objects in a room, it loses energy (volume) each time it does so. In highly reverberant rooms such as churches (the Hagia Sophia in Turkey has something like a 10-second reverberation time!), the reflections are numerous because they don’t lose as much energy with each bounce, so signals originating from the space will retain less information because previous signals are still bouncing around. So, the greater the reverberation, the less signal and greater noise.
But, not all signals are equal. Acoustic spaces (and musical instruments) are ideally designed to give preferences to a certain frequency range, which for speech is about 1000-5000 Hz. We can test these “frequency preferences” by measuring how the room behaves to specific frequencies. This measurement is called a frequency response. One way to do this is by playing a sine sweep—a sine wave starting from 0 Hz and constantly increasing (linearly or logarithmically) until ending at 25000 Hz (or whatever desired range)—and recording it in the room. This method requires no transformation to a frequency domain because time and frequency are tied! The recorded amplitude is the amplitude response of the room. From this, it should be clear that a room and a musical instrument alike are both types of filters.
However, speakers have frequency responses, too, so unless that response is known (and even if it is), the sine sweep can pose problems and return inaccuracies. Fortunately, there is another, more clever way to do this: by an impulse function, such as one of those mentioned in the post below. Refresher: an impulse function \delta(t-a) is defined as zero everywhere that t does not equal a (t is time, a is some instant of time), and non-zero where t=a (infinity in the continuous case and 1 in the discrete case). An impulse function is not differentiable, but it is integrable (in the continuous case), and its integral is equal to 1.
Now, what does an impulse sound like? This two-fold jump in amplitude from 0 to maximum value to 0 again is colloquially called a tone burst: it’s like dropping the needle on a record player, or sampling audio at non-zero endpoints and causing a speaker to emit a ‘click’—the sound of it trying to move infinitely fast (because velocity is the derivative of position! So it all comes down to differentiability!) from one position to another. This is also known as clipping, an undesirable effect in virtually every aspect of life save hygiene (okay, there may exist others). What does clipping have to do with the frequency responses of acoustic spaces? Well, what is the frequency response of an impulse?
This is quickly calculated by taking the Fourier transform of \delta(t-a), which is equal to exp(-ia\omega), where \omega is frequency. When a=0, which is the case for a single impulse, and since time is relative (don’t sue; yeah I’ve seen the article about the neutrinos), it’s okay to call a=0 in most situations. Thus, F{\delta(t-0)}=exp(-i0\omega)=1 for all \omega. This is called a flat (frequency) response, the desired response for speakers, and when we apply it to a room and record the results, the Fourier transform of the results shows the frequency response of the room!
The sound of an impulse is that of white noise, which has equal energy spread to all frequencies, much like white light contains the entire visible spectrum. The Fourier transform of \delta(t-a) is exp(-ia\omega) because of the Shifting theorem, which states that F{x(t-a)}=F{x(t)}*exp(-ia\omega). Finally, the Fourier transform of a finite-time-domain signal is infinite, and the Fourier transform of an infinite-time-domain signal is finite. This is a result of Gibb’s Phenomenon, the subject of my next post!
Happy DSP’ing!
Posted: August 25th, 2011 | Author: Gina Collecchia | Comments Off on Kronecker vs. Dirac delta functions
Delta functions are used to sample time-domain signals in signal processing, but their type is often unstated or incorrectly specified. A Dirac delta function is a continuous function d(t-a) whose integral is exactly equal to 1 and is only nonzero at t=a. Hence, it is infinitesimal in width (its width approaches 0) and infinitely tall (its amplitude approaches infinity). The Dirac delta is applied to analog, continuous signals to return a continuous scaled impulse function at a specified instant of time (indicated by the domain of the Dirac delta). This is done by taking the integral over all values of the signal x(t) times the Dirac delta centered at a, d(t-a). The resulting function is a continuous function equal to x(a)*d(t-a).
The Kronecker delta function is similarly infinitesimally thin, but its amplitude is equal to 1, not its area. The function d[t-a] is equal to 1 when t=a and 0 otherwise, i.e., when t!=a. The Kronecker delta is a discrete function. It applies a discrete impulse to a continuous signal, and returns the original amplitude of the signal. Therefore, the resulting function is discrete, and equal to x[a]*d[t-a].
Since they can be written the same way (the square brackets to indicate that a function is discrete are not required), most texts will just call the delta function the Dirac type, if any. But if this were so, a discrete signal would have all infinite (positively and negatively) amplitudes! So, the difference is significant.
Wish I could have TeX’ed that but hopefully you found this helpful. The concept of a sampled function is really what is important here, and it represents the amplitude of a continuous signal at specific points of time. But a Dirac returns a continuous sampled function, and a Kronecker returns a discrete one.


